【機械学習】勾配降下法についてざっくりまとめ【Python】

今年は機械学習(学習モデルの作り方)について勉強漬けの年となりました.
だがしかし、「じゃあぱっと作り方や計算式も引き出せるよね」って言われると…
…無理でした.
今年から勉強方法も一新して、ノートで少しずつまとめたりなど個人的に楽しいと
思えるインプットをやってきましたが、それ故にアウトプットが不十分になってしまいました.
ということで紙のノートなどにまとめた資料を総括して、頭の中から引き出せるようにこれから年末までを目標に書いていこうかと思います.
今回はその記念すべき第一回となります.

ちなみに学習する上で中心となった参考書はこちらです.
最短コースでわかる　ディープラーニングの数学 
これから書く内容についても、この書籍受けよりな部分が多々あります…
時間があればそちらを読んだ方が断然わかりやすいので、ぜひチェックしてみてください.

勾配降下法とは

　関数の谷底をゴールとし、少しずつ進む＝最小値を目指す方法です.
ある2次関数L(x、y)のグラフを例とします.

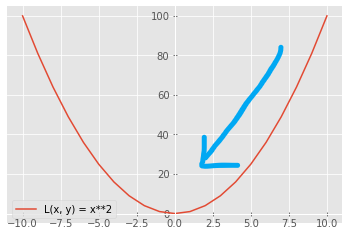
図は\(L(x, y) = x^{2} \)の2次関数となっていますが、式については正直なんでも良いです.
今回は谷底に向かう様子が分かりやすくするためにこの式にしています.

続いて、勾配降下法の手順を以下にまとめます.
　　① 初期位置\((u_{0}, v_{0}) \)を決める.
　　② ①で定めた位置から\(L(x, y)\)を一番大きく減少させる方向を見つける.
　　⇒ベクトルにおける向きを表す.
　　③ ②の向きに合わせて微小量だけ\((u_{0}, v_{0}) \)の値を変化、この値を\((u_{1}, v_{1}) \)とする.
　　⇒ベクトルにおける大きさを表す.
　　　また、「微小量だけの値を変化」とは全微分によって表せる.(後述)
　　④ 新しい点(u1, v1)を基に②、③の処理を繰り返す.

以上の工程より、向きと大きさを持つことからその移動量をベクトルとして考えることができます.

以下、勾配降下法の②,③について具体的に解説していきます.

② (uk, vk)から次の点(uk+1, vk+1)に移動するためにどのような向きに移動すれば良いか？(最も効率的に移動したい)

前提：
　・移動量は微小量である.
　・その移動量の大きさは一定(\(\sqrt{(du)^2+(dv)^2}\) = (一定))である.

これらの前提により、全微分の公式を使うことができます.
\(dL(u_{k}, v_{k}) = L_{u}(u_{k}, v_{k})du + L_{v}(u_{k}, v_{k})dv \)
この式と以下の図を見てもらえれば、全微分とベクトルの関係性がなんとなぁく見えてくると思います…

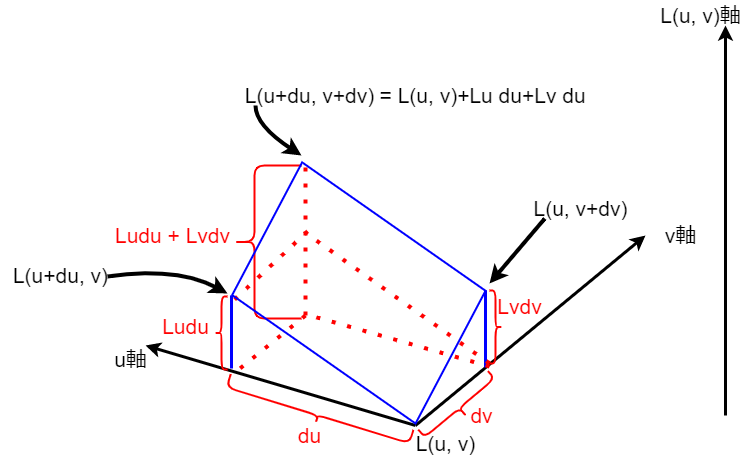
続いて、以下のように右辺をベクトルの内積として考えてみます.
\(dL(u_{k}, v_{k}) = (L_{u}(u_{k}, v_{k}), L_{v}(u_{k}, v_{k})) · (du, dv) \)
また、内積の公式より２つのベクトルのなす角をθとすると
\(dL(u_{k}, v_{k}) = (L_{u}(u_{k}, v_{k}), L_{v}(u_{k}, v_{k})) · (du, dv) = |(L_{u}, L_{v})| |(du, dv)| \cos\theta \)
と表せます.
点\((u_{k}, v_{k})\)の位置にいる瞬間であるため、\(L_{u}\)と\(L_{v}\)は定数です.
これにより\(\cos\theta \)のみが変数となります.

　したがって内積と角度θの関係よりcos180°(=-1)の時、つまり\((u_{k}, v_{k})\)と\((du, dv)\)二つのベクトルがちょうど逆向きの時に最小値をとることができます.
逆向きに進むことでグラフの底へと向かっていくイメージですね.
\(dL(u_{k}, v_{k}) = -|(L_{u}, L_{v})| |(du, dv)| \)

③ 次に大きさ(移動量)を決める

再度\(L(x, y) = x^{2} \)を見る
以下の図の矢印はそれぞれの点の微分値(\(L(x, y) = 2x \)に代入した値)に0.1をかけた値を移動量として図示しています.(xが0で最小です)

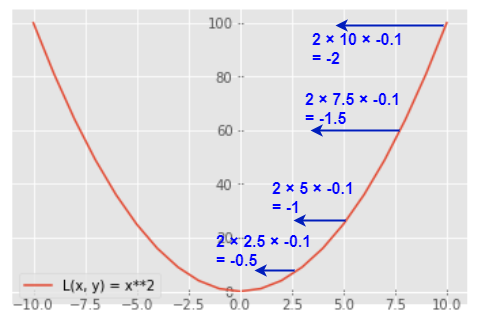
図を見ると以下のことが分かります.
・x = 0から離れている：微分値は大きく、移動量も大きい
・x = 0に近い：微分値は小さく、移動量も小さい

つまり、各微分値に負の一定値をかけた値を移動量とすると、程よい移動量になります.

ここまで来たら次は公式の紹介です.

勾配降下法の公式

以上を踏まえて、勾配降下法の式を以下に示します.

$$
\begin{pmatrix} u_{k+1}\\ v_{k+1}\end{pmatrix} = \begin{pmatrix} u_{k}\\ v_{k}\end{pmatrix} – α\begin{pmatrix} L_{u}(u_{k}, v_{k})\\ L_{v}(u_{k}, v_{k})\end{pmatrix}
$$

式中のαは学習率で、③における-0.1をかける工程そのものです.
また、\((u_{k}, v_{k}) \)に対して\(α(L_{u}(u_{k}, v_{k}), L_{v}(u_{k}, v_{k})) \)で引いているのは②における「逆向きに進む」の意味合いです.

学習率について

以下のように、偏った設定にはそれぞれデメリットがあります.
・学習率が大きすぎる場合：移動量が増えることにより、最小値(底)を通り過ぎてしまいます.
・学習率が小さすぎる場合：移動量が微小になり、収束するまでが遅くなります.

試行回数について

勾配を繰り返す回数を指します.
学習率が小さい場合は試行回数を増やすことで収束まで辿りつかせることができ、逆に少ないと十分な精度が出ずに終わります.
学習率が大きすぎるかつ試行回数も多いと過学習となり発散してしまうので、学習率と同様に適切な設定が必要にります.

おわりに

今回は勾配降下法についてざっくりまとめました.
備忘録として自分なりにしっかりまとめたつもりなので、今後役に立ってくれることにも期待.
引き続き今年のインプットの総括を行っていきます.

ちなみに、過去にも線形回帰についてまとめています.(後程リファイン予定ですが)