【機械学習】ロジスティック回帰分析(2値分類)についてざっくりまとめ【Python】

前回に引き続き、機械学習についてまとめていきます.
今回はロジスティック回帰(の2値分類)について、特に勾配降下法への適用方法について書いていくつもりです.
前提知識として勾配降下法が必要になるので、良ければ前回の記事も御覧ください.

ちなみに学習する上で中心となった参考書はこちらです.(前回同様)
最短コースでわかる　ディープラーニングの数学
これから書く内容についても、この書籍受けよりな部分が多々あります…
時間があるならそちらを読んだ方が断然わかりやすいはずなので、こちらもぜひチェックしてみてください.

ロジスティック回帰とは

　一言で表すなら「ある事象が起こる確率」を予測する手法です.
「陽性(1)か陰性(0)か」に分ける問題を2値分類、「猫、犬、人」のように３つ以上に分ける問題を多値分類と呼びます.
今回は比較的簡単な2値分類について書いていきます.

回帰モデルと分類モデルの違い

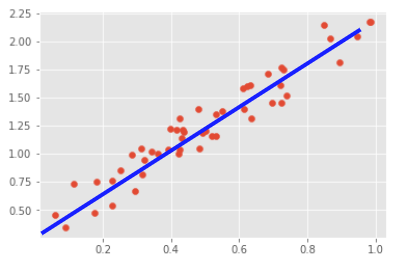
　 散布したデータに対して良い感じに線を引くのはどちらも同じですが、その意味合いが異なります.

　・回帰問題：説明変数(図中の赤点)である個々の点から目的変数の傾向を予測する直線を引きます.

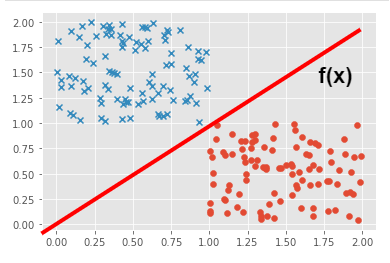
　・分類問題：説明変数(図中の〇×)である個々の点から目的変数のグループを予測する直線(境界線)を引きます.

学習方法

勾配降下法を使います.

機械学習プロセス

　以下の①～④の順に重みベクトル\(w_{0},w_{1},w_{2}\)の最適パラメータを求めるアルゴリズムを作っていきます.
①特徴量から正解値(yt)を求めるための予測モデルの作成
　⇒・カテゴリ変数の作成
　　・学習用データ、検証用データに分ける
②予測値(yp)と正解値(yt)から計算可能な損失関数(L)の作成
③勾配降下法に向けた準備として、損失関数(L)の微分計算を行う
④ ③の計算結果を基に勾配降下法を使って計算する

では始めます.

①予測モデルの作成

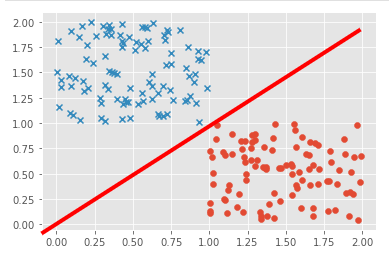
　下図のような、散布したデータをちょうど２つに分けるような線を引きたいとします.

その線形関数を以下のように定義します.
$$u = w_{0} + w_{1}\cdot x_{1} + w_{2}\cdot x_{2}$$
この時、uの値が仮に0か1と出力してくれる関数ならばうまく分類をしてくれそうな感じがします.
しかし、0か1の2パターンしか出力できない離散的な関数となると、そもそも微分ができません.
勾配降下法で学習を行う場合、損失関数は微分可能な関数である必要があります.
　
そこで関数uにシグモイド関数を合成することにします.
$$f(x) = \displaystyle\frac{1}{1 + exp(-x)}$$

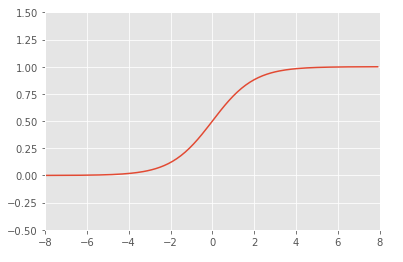
これで結果を0～1の値に丸め込むことができます.
それに担い\(u = w_{0} + w_{1}\cdot x_{1} + w_{2}\cdot x_{2}\)と\(f(x)\)を合成関数\(yp = f(u)\)と定義しておきます.

また、以下の図は散布図に決定境界を示す直線を引いたものになります.

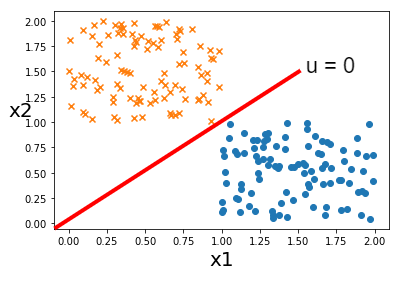
図中の「×」をclass=0、「〇」をclass=1としています.
中央の線は\(u = w_{0} + w_{1}\cdot x_{1} + w_{2}\cdot x_{2} = 0\)の直線です.
この時、x軸がx1、y軸がx2であり特徴量の散布図を表していることに注意しましょう.
関数の方も分かりやすくするために左辺を\(x_{2}\)とした式に変形しておきます.
$$x_{2} = (w_{1}/w_{2})\cdot x_{1} + (w_{0}/w_{2})$$

次にu = 1,u = 2…のようにuの値を変化させてみましょう.
その時の直線を図に追加していきます.

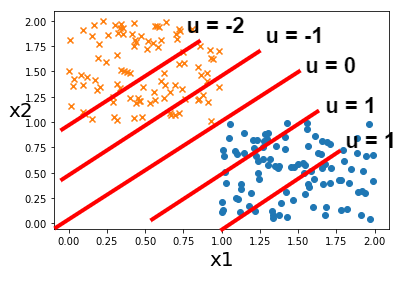
左辺を\(x_{2}\)とした式において切片が増減することにより、直線の場所が変化していることが見てわかるかと思います.

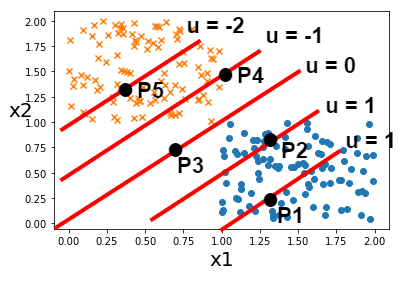
さらに、各直線に対して任意の点(P1～P5)をとり、それぞれの点におけるuの値とその値にシグモイド関数をかけたf(u)の値の関係を見ていきます.

シグモイド関数の計算は下記のサイトでさっと行います.
https://keisan.casio.jp/exec/system/1515561226
P5：f(u=-2) = 0.12
P4：f(u=-1) = 0.269
P3：f(u= 0) = 0.5
P2：f(u= 1) = 0.731
P1：f(u= 2) = 0.88
P5 + P1 = 1、P4 + P2 = 1であり、P5である確率が0.12で逆にP1である確率は0.88であることを指しています.
また、ちょうど真中であるP3は約50%の半々であると捉えることができるはずです.
さらにこの式は連続的な値になるため微分も可能です.

以上より、f(u)の値を予測式とすることにします.

ちなみに、関数uは以下のように内積を使うことで式を簡潔にすることができます.(この時\(w_{0}\)にかけている1をダミー変数と呼びます.)
\begin{align*}
&u = w_{0} + w_{1}\cdot x_{1} + w_{2}\cdot x_{2}= w_{0}\cdot 1 + w_{1}\cdot x_{1} + w_{2}\cdot x_{2}\\
\\
&　= (w_{0}, w_{1}, w_{2})・(1, x_{1}, x_{2})
\end{align*}

以上を踏まえて、入力値xからypを求めるまでの流れを合成関数として以下にまとめておきます.

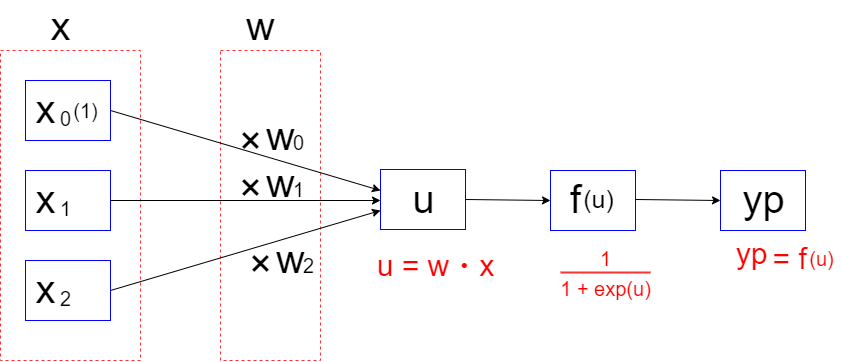
\begin{align*}
&・u = w_{0} + w_{1}\cdot x_{1} + w_{2}\cdot x_{2}\\
&\\
&・f(x) = \displaystyle\frac{1}{1 + exp(-x)}\\
&\\
&・yp = f(u)\\
\end{align*}

②損失関数(L)の作成

　①で定義した式を使って損失関数を作っていきましょう.

まず初めに\(yp = f(u) = f(w_{0} + w_{1}\cdot x_{1} + w_{2}\cdot x_{2})\)の値を正解値ytを求める確率とみなします.(ちなみにytの解は0か1しかありません.)
仮にyt = 1の確率がypなら、yt = 0の確率は1-ytになります.
更にこの時の確率値を以下のように定義しておきます.

\(\begin{equation} \label{eq: cases f}P(yt, yp) = \begin{cases} yp & \text{$yt = 1$のとき} \\ 1 – yp & \text{$yt = 0$のとき} \end{cases} \end{equation}\)
\(= f(u) = f(x\cdot w)\)

この確率値を用いて、これから最尤推定により損失関数を求めていきます.

・最尤推定とは：

　先程のPの式について、例えば入力値として5つのデータが渡された場合を考えてみます.
この時、1回目と3回目がyt = 1、残りが0となる時の確率は、以下のように各事象の確率の積で表すことができます.
\(\begin{equation}P(yt=1, yp )\cdot P(yt=0, 1 – yp )\cdot P(yt=1, yp )\cdot P(yt=0, 1 – yp )\\
\cdot P(yt=0, 1 – yp )\\
　　= yp^{2}\cdot (1 – yp)^{3}\end{equation}\)

観測値ytをypの式で表したこの式を尤度関数と呼びます.
更に、以下のように式全体に対数を取ってみましょう.
\(\begin{equation}\log (P(yt=1, yp )\cdot P(yt=0, 1 – yp )\cdot P(yt=1, yp )\cdot P(yt=0, 1 – yp )\\
\cdot P(yt=0, 1 – yp ))\\
　= \log (P(yt=1, yp )) + \log (P(yt=0, 1 – yp )) + \log (P(yt=1, yp )) \\
　　　　+ \log (P(yt=0, 1 – yp )) + \log (P(yt=0, 1 – yp ))\end{equation}\)

ちなみにこの時の式を対数尤度関数と呼びます.

こうすることで何が嬉しいかと言いますと、理由は主に二つあります.
　1. 対数を取ると式全体の掛け算が足し算に代わり、計算(主に微分)がしやすくなるため
　2. 大量のデータに対して掛け算を行うと値が小さくなりすぎてアンダーフローを起こしてしまうため

そしてこの対数尤度関数をパラメータ(ここではyp)で微分し、ちょうど微分値が0になる時のパラメータを最も尤もらしい値として推定することを最尤推定と呼びます.
(前置きが長かったですが、その意味自体は非常にシンプルなんです)
微分値が0になる時というのも、勾配降下法とコンセプトが似てますね.

さて、つまりはこの対数尤度関数を損失関数として使えば良い感じになりそう…というのは何となくわかるかと思いますが、一つ問題があります.
入力値によってypか1-ypかで式自体が変わってしまい、一意に式が定まりません.
なにより微分も大変です.

そこで今度は交差エントロピーの登場です.

・交差エントロピー：

　交差エントロピーとは、二つの確率分布がどれくらい離れているか表す尺度のことです.
\begin{equation} ce = −\sum\limits_{x}^{} P(x)\log Q(x)\end{equation}

今回は1か0かの2値分類ですので、実際には以下の式を使います.
\begin{equation}ce = −yt \log yp − (1 − yt)\log (1 − yp)\end{equation}

ちなみに、式にマイナスが付いているのは尤度が本来、値を最大にすることが目的であり、勾配降下法における最小値を求める計算に合わせるために式全体に-1をかけて帳尻合わせをしているためです.

それでは試しにyt = 1,yt = 0を代入してみましょう.
・yt = 1の時
\( −1 \log yp − (1 − 1)\log (1 − yp) =- \log yp\)

・yt = 0の時
\(−0 \log yp − (1 − 0)\log (1 − yp) =- \log (1 − yp)\)

結果を見てもらえば分かる通り、０か1しかとらない条件に非常にマッチしています.

以上の結果を基に、損失関数を定義します.
(といっても対数尤度関数をちょっと改良するだけですが.)
\(L(w_0, w_1, w_2) = -\displaystyle\frac{1}{M}\sum\limits_{m=0}^{M-1} {yt^{(m)}\cdot \log (yp^{(m)}) +
(1 – yt^{(m)})\cdot \log (1 – yp^{(m)})} \)
\(= \displaystyle\frac{1}{M}\sum\limits_{m=0}^{M-1} ce^{(m)}\)

一般化するにあたって、入力データ件数をMとして拡張しています.
また、Mで割って平均をとることでデータ件数の影響をなくしています.

これにて損失関数の作成は終わりです.

③損失関数(L)の微分計算

　微分計算により損失関数の極小値を求めることで最尤推定を行います.
この時、変数wについて全微分を行う必要があるためかなり複雑そうに思えるかもしれません.
しかし、式の工程をこれから示すように可視化していくことでだいぶわかりやすくなるはずです.

まず初めに入力値xからypを求めるまでの流れを整理して以下にまとめます.

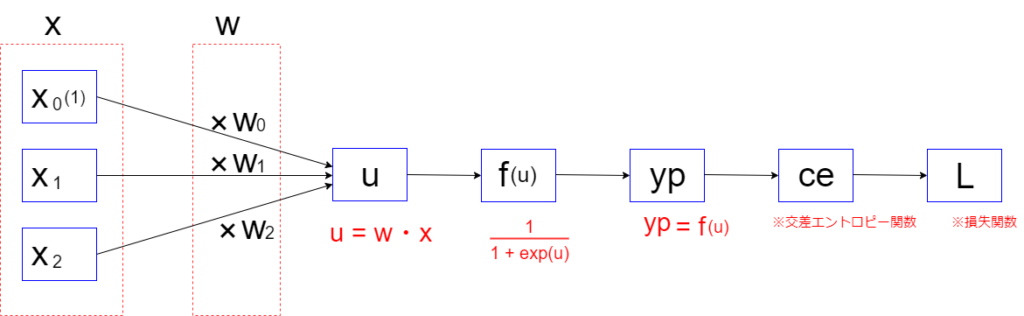
さらに以下のように式も並べてみます.

\begin{align*}
&yp = f(u) = \displaystyle\frac{1}{1 + exp(-u)}\\
&\\
&ce = – yt\cdot \log (yp) – (1 – yt)\cdot \log (1 – yp)\\
&\\
&L(w_0, w_1, w_2) = -\displaystyle\frac{1}{M}\sum\limits_{m=0}^{M-1} {yt^{(m)}\cdot \log (yp^{(m)}) +
(1 – yt^{(m)})\cdot \log (1 – yp^{(m)})} \\
&= \displaystyle\frac{1}{M}\sum\limits_{m=0}^{M-1} ce^{(m)}
\end{align*}

入力値xから\(u,yp,ce\)と式が段々と続いていき、最後に損失関数に流れていく過程全体を一つの合成関数として考えることができます.

それではまず、損失関数Lを重みベクトル\(w_{1}\)で偏微分していきます.

$$\displaystyle\frac{\partial L}{\partial w_{1}} = \displaystyle\frac{dL}{du}\cdot \displaystyle\frac{\partial u}{\partial w_{1}}$$

上の式を見てください.
式についてざっくり説明すると、左辺は「関数Lを\(w_{1}\)で偏微分する」という意味で、右辺はその式を分解して「関数Lをuで微分する」と「関数uを\(w_{1}\)で偏微分する」の式にしています.(右辺を掛け算するとuを打ち消し合って左辺になる)
ここから
①右辺の右の式
②右辺の左の式
でそれぞれ個別に計算していきましょう.

①\(\displaystyle\frac{\partial u}{\partial w_{1}}\)の式

関数\(u(w_{0},w_{1},w_{2}) = w_{0} + w_{1}\cdot x_{1} + w_{2}\cdot x_{2}\)なので、\(w_{1}\)について微分すると以下の解が出ます.

$$\displaystyle\frac{\partial u}{\partial w_{1}} = x_{1}$$

②\(\displaystyle\frac{dL}{du}\)の式

この式を合成関数としてさらに分解します.

$$\displaystyle\frac{dL}{du} = \displaystyle\frac{dL}{d(yp)}\cdot \displaystyle\frac{d(yp)}{du}$$

まずは\(\displaystyle\frac{dL}{d(yp)}\)について、損失関数Lは交差エントロピー関数なので以下のようにして計算していきます.

\begin{align*}
&\displaystyle\frac{dL}{d(yp)} = \displaystyle\frac{d(ce)}{d(yp)} = (- yt\cdot \log (yp))^{\prime}{(1 – yt)\cdot \log (1 – yp)}^{\prime}\\
&\\
&= – \displaystyle\frac{yt}{yp} – \displaystyle\frac{(1 -yt)(-1)}{1 – yp} = \displaystyle\frac{-yt(1 – yp)+yp(1 – yt)}{yp(1 – yp)}\\
&\\
&= \displaystyle\frac{yp – yt}{yp(1 – yp)}
\end{align*}

そして関数ypですが、こちらはシグモイド関数の微分なので

$$\displaystyle\frac{d(yp)}{du} = yp(1 – yp)$$

よって、この二つをかけると以下のようにシンプルな結果になります.

\begin{align*}
&\displaystyle\frac{dL}{du} = \displaystyle\frac{dL}{d(yp)}\cdot \displaystyle\frac{d(yp)}{du} = \displaystyle\frac{yp – yt}{yp(1 – yp)}\cdot yp(1 – yp)\\
&\\
&= yp – yt\\
\end{align*}

さらにyd = yp – ytと置き、誤差ydを定義すると、①②の結果より

$$\displaystyle\frac{\partial L}{\partial w_{1}} = x_{1}\cdot yd$$

これに添え字とΣを戻してあげると

$$\displaystyle\frac{\partial L}{\partial w_{1}} = -\displaystyle\frac{1}{M}\sum\limits_{m=0}^{M-1} x_{1}^{(m)}\cdot yd^{(m)}$$

\(w_{0},w_{2}\)の微分結果も添え字が変わるだけで同じなので、式を一般化すると以下のようになります.

$$\displaystyle\frac{\partial L}{\partial w_{i}} = -\displaystyle\frac{1}{M}\sum\limits_{m=0}^{M-1} x_{i}^{(m)}\cdot yd^{(m)}
\displaystyle_{(i = 0, 1, 2)}$$

④勾配降下法の適用

　最後に③の結果を勾配降下法に落とし込みましょう.
最適なパラメータを求めるために何回も勾配降下法を繰り返す必要があるので、それをk回繰り返すとして以下のように式を定義します.

$$w_{i}^{(k+1)} = w_{i}^{(k)}-\displaystyle\frac{\alpha}{M}\sum\limits_{m=0}^{M-1} x_{i}^{(m)}\cdot yd^{(m)}
\displaystyle_{(i = 0, 1, 2)}$$

これにて2値分類における勾配降下法の完成です.

終わりに

　今回は2値分類についてまとめました.
kerasなどのフレームワークを使えれば機械学習はOK..かもしれませんが、要件に合った学習モデルを作る場合には根本のロジックへの理解が必要不可欠ですし、知見を広げていくにも数式が理解できなければいかなる良書にも手が出せません.
勾配降下法という根本はどこも同じなので、こういった基礎部分だけでもしっかり固めた上で知見を広めていきたいです.