【機械学習】ロジスティック回帰分析(多値分類)についてざっくりまとめ【Python】

前回は2値分類についてまとめました.
今回はその拡張版とも言える多値分類について書いていきます.

前回の2値分類の続きとして書いていくので、良ければ先にこちらをご覧になってください.

ちなみに学習する上で中心となった参考書はこちらです.(前回同様)
最短コースでわかる　ディープラーニングの数学
これから書く内容についても、この書籍受けよりな部分が多々あります…
時間があるならそちらを読んだ方が断然わかりやすいはずなので、こちらもぜひチェックしてみてください.

それでは始めます.

多値分類とは

　前回説明した2値分類は「陽性(1)か陰性(0)か」の２択に分ける問題でした.
多値分類は「猫、犬、人」のような３つ以上に分類したい問題を指します.

2値分類との違いは？

　アルゴリズムの違いに着目して書いていきます.
2値分類は「０から1までの確率値を出力する分類器」を一つだけ使っていましたが、多値分類ではそんな分類器をクラスの数だけ用意して並列に処理を行います.
そして、その結果最も確率値の高い分類器に対応するクラスをモデル全体の予測値とするのです.

例えば犬、猫、人のクラスを分類したい時、
　犬 = 0 = (1, 0, 0)
　猫 = 1 = (0, 1, 0)
　人 = 2 = (0, 0, 1)
のように0と1で扱える３次元ベクトルに変換します.
この変換のことをOneHotベクトル化と呼び、３次元ベクトルの各列を求める分類器を用意します.
そして入力データにそれらの式を適用し、計算した結果、最も高い確率の列をクラスとして割り当てるのです.(この手法を1対多分類器とも呼びます)
簡単な図も以下に載せます.

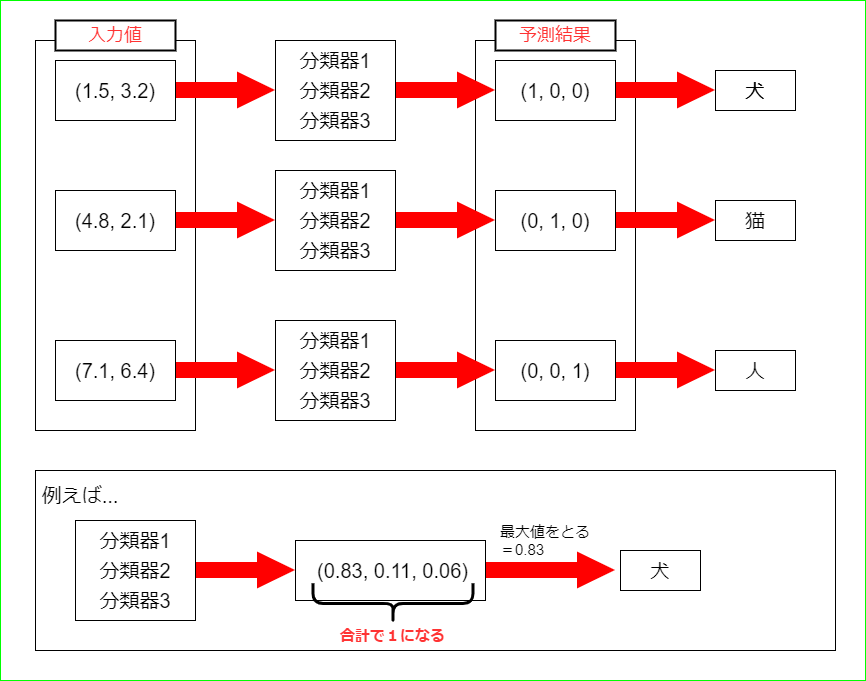
一見複雑ですが、大本は2値分類とやってることは同じなんです.

また、さらに以下の２点が2値分類と異なります.
1.重みベクトル⇒重み行列
2.シグモイド関数⇒softmax関数

違いとしては以上になります.
そうです.これだけなんです.

次は後述の「1.」,「２.」についてより詳しく説明していきます.
(以降は犬、猫、人の３クラスの分類問題として話を進めていきます)

1.重み行列について

はじめに2値分類で使われる重みベクトルからおさらいしましょう.

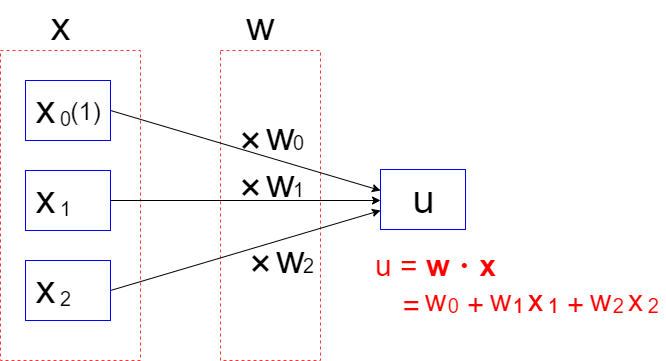
続いて多値分類で使われる重み行列です.

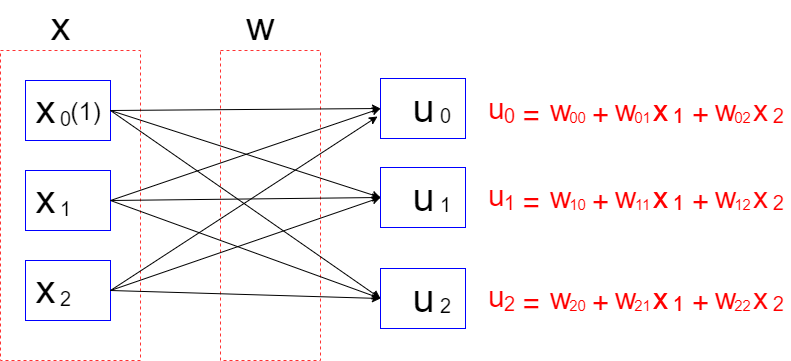
行列と名乗るその意味通り、重みが行列式によって表されています.
uの式について詳細をまとめます.

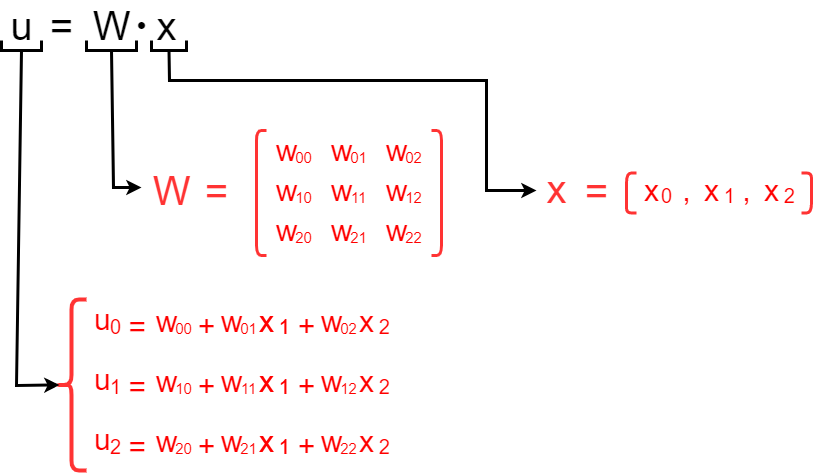
複数の重みベクトルが集まって一つの行列式になっており、これと入力値(ベクトル)との積を計算することで分類器の数に合った内積を同時に導出することが可能になります.

2.softmax関数について

　２値分類では活性化関数としてシグモイド関数を使って確率値を求めていました.
多値分類では代わりにsoftmax関数と呼ばれるシグモイド関数の拡張版のようなものを使います.
活性化関数にかける前の式uが複数ある(分類したいクラスが３つ以上ある)場合、softmax関数をかけることで、その合計を1(100%)とする確率値に変換してくれます.
以下に式を図示します.

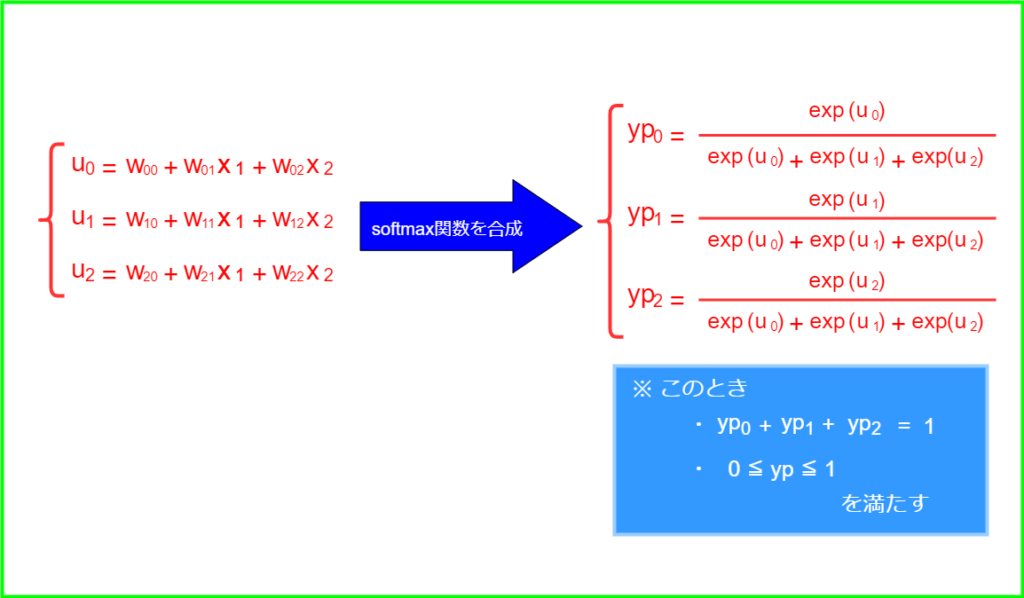
以上を踏まえて、次からは損失関数を定義していきます.

損失関数の作成

　ここは2値分類の時と考え方は同じです.
多値分類における対数尤度関数は以下になります.(2値分類の交差エントロピーの拡張版です)

\begin{align*}
&ce = \sum\limits_{i=0}^{2} {yt_{i}\cdot \log (yp_{i})} \\
\end{align*}
繰り返しますが、今回は犬、猫、人の３クラスの分類問題として話を進めています.
そのため(i = 0,1,2)としています.
ちなみに２値分類の場合の対数尤度関数は以下でした.
$$ce = – yt\cdot \log (yp) – (1 – yt)\cdot \log (1 – yp)$$

試しに正解値が(0, 1, 0)の場合(=猫)で考えてみましょう.
\(\sum\limits_{i=0}^{2} {yt_{i}\cdot \log (yp_{i})} = yt_{0}\cdot \log (yp_{0}) + yt_{1}\cdot \log (yp_{1}) + yt_{2}\cdot \log (yp_{2}) )\)
\(= 0\cdot \log (yp_{0}) + 1\cdot \log (yp_{1}) + 0\cdot \log (yp_{2}) \)
\(= \log (yp_{1}) \)

\(log 1 = 0\)なので正解値と同じ添字を持つypを求めることができました.

以上より損失関数を定義します.
\(L(w_0, w_1, w_2) = -\displaystyle\frac{1}{M}\sum\limits_{m=0}^{M-1}\sum\limits_{i=0}^{2} {yt_{i}^{(m)}\cdot \log (yp_{i}^{(m)})}\)

損失関数の微分

　基本的なやり方は2値分類の場合と同じです.
ただし、重みベクトルをクラス数分(今回だと３セット)増やした重み行列として(w_{i j})を偏微分していく必要があります.
\(w_{1 2}\)の偏微分を例として、入力値xからypを求めるまでの流れを一旦整理しましょう.

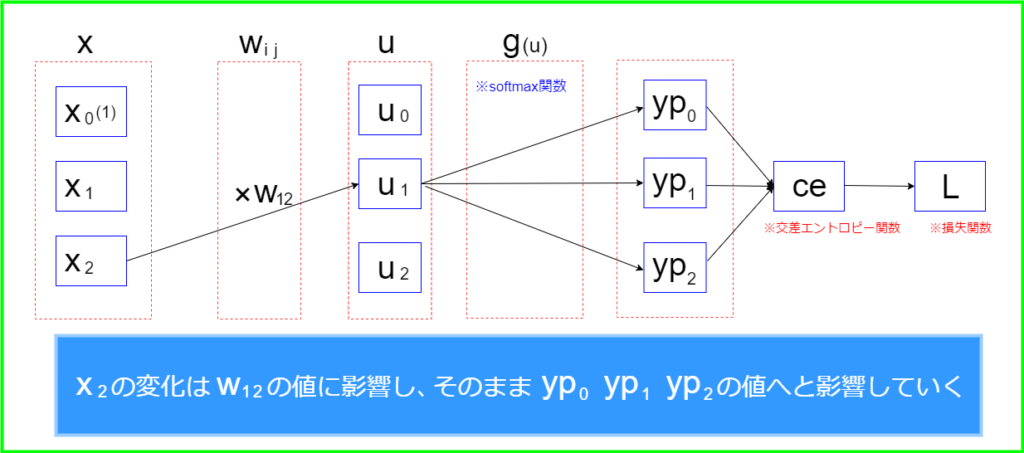
図のように、\(w_{1 2}\)を偏微分する際に影響を与える場所(式中に\(w_{1 2}\)が含まれる)を確認しておくと合成関数として分割しやすくなります.

それでは最初に関数Lを\(w_{1 2}\)で偏微分する式を合成関数として分解します.
$$\displaystyle\frac{\partial L}{\partial w_{12}} = \displaystyle\frac{\partial L}{\partial u_{1}}\cdot \displaystyle\frac{\partial u_{1}}{\partial w_{12}}$$

ここから
①右辺の右の式
②右辺の左の式
でそれぞれ個別に計算していきましょう.

①\(\displaystyle\frac{\partial u_{1}}{\partial w_{12}}\)

以下の式について(w_{1 2})を偏微分します
$$u_{1} = w_{10} + w_{11}x_{1} + w_{12}x_{2}$$
結果は以下となります.
$$\displaystyle\frac{\partial u_{1}}{\partial w_{12}} = x_{2}$$

②\(\displaystyle\frac{\partial L}{\partial u_{1}}\)

以下のように合成関数として更に分解します.
$$\displaystyle\frac{\partial L}{\partial u_{1}} = \displaystyle\frac{\partial yp_{i}}{\partial u_{1}}\cdot\displaystyle\frac{\partial L}{\partial yp_{i}}\displaystyle_{(i = 0, 1, 2)}$$

ここで、\(u_{1 }\)は\(yp_{0}\)、\(yp_{1}\)、\(yp_{2}\)のそれぞれに影響していて、\(yp_{0}\)、\(yp_{1}\)、\(yp_{2}\)はLの値に影響していることを意味しています.

③右辺の右の式
④右辺の左の式
として、個別に更に微分していきます.

③\(\displaystyle\frac{\partial L}{\partial yp_{i}}\displaystyle_{(i = 0, 1, 2)}\)

\(L(yp_{0}, yp_{1}, yp_{2}) = ce = – ( yt_{0}\cdot \log (yp_{0}) + yt_{1}\cdot \log (yp_{1}) + yt_{2}\cdot \log (yp_{2}))\)
なので\(yp_{0}\)、\(yp_{1}\)、\(yp_{2}\)についてそれぞれ偏微分を行うと
\(\displaystyle\frac{\partial L}{\partial yp_{0}} = -\displaystyle\frac{\partial ce}{\partial yp_{0}} = -\displaystyle\frac{yt_{0}}{yp_{0}}\)

\(\displaystyle\frac{\partial L}{\partial yp_{1}} = -\displaystyle\frac{\partial ce}{\partial yp_{1}} = -\displaystyle\frac{yt_{1}}{yp_{1}}\)

\(\displaystyle\frac{\partial L}{\partial yp_{2}} = -\displaystyle\frac{\partial ce}{\partial yp_{2}} = -\displaystyle\frac{yt_{2}}{yp_{2}}\)

④\(\displaystyle\frac{\partial yp_{i}}{\partial u_{1}}\)

こちらはsoftmax関数の偏微分です.
以下にsoftmax関数の微分結果を載せます.
$$\begin{equation} \label{eq: cases f}\displaystyle\frac{\partial yp_{j}}{\partial u_{i}} = \begin{cases} yp_{i}(1 – yp_{i}) & \text{(i = j)} \\ -yp_{i}\cdot yp_{j} & \text{(i $\neq$ j)} \end{cases} \end{equation}$$
したがって
$$\displaystyle\frac{\partial yp_{0}}{\partial u_{1}} = -yp_{1}\cdot yp_{0}$$
$$\displaystyle\frac{\partial yp_{1}}{\partial u_{1}} = yp_{1}(1 – yp_{1})$$
$$\displaystyle\frac{\partial yp_{2}}{\partial u_{1}} = -yp_{1}\cdot yp_{2}$$

③、④の結果を\(\displaystyle\frac{\partial L}{\partial u_{1}} \)に代入します.
\begin{align*}
&\displaystyle\frac{\partial L}{\partial u_{1}} = \displaystyle\frac{\partial L}{\partial yp_{0}}\cdot\displaystyle\frac{\partial yp_{0}}{\partial u_{1}} + \displaystyle\frac{\partial L}{\partial yp_{1}}\cdot\displaystyle\frac{\partial yp_{1}}{\partial u_{1}} + \displaystyle\frac{\partial L}{\partial yp_{2}}\cdot\displaystyle\frac{\partial yp_{2}}{\partial u_{1}}\\
&\\
&= -\displaystyle\frac{yt_{0}}{yp_{0}}(-yp_{1}\cdot yp_{0})-\displaystyle\frac{yt_{1}}{yp_{1}}\cdot yp_{1}(1 – yp_{1})-\displaystyle\frac{yt_{2}}{yp_{2}}(-yp_{1}\cdot yp_{2})\\
&\\
&= {yt_{0}}\cdot yp_{1}-{yt_{1}}(1 – yp_{1})+{yt_{2}}\cdot yp_{1}\\
&\\
&= -{yt_{1}}+{yp_{1}}(yt_{0} + yt_{1} + yt_{2})\\
\end{align*}

ここで、\(yt_{0} + yt_{1} + yt_{2}\)の式はOneHot化したデータなので総和は1になります.
したがって
$$\displaystyle\frac{\partial L}{\partial u_{1}}= {yp_{1}}-yt_{1}$$

$$\displaystyle\frac{\partial L}{\partial u_{i}} = {yp_{i}}-yt_{i}\displaystyle_{(i = 0, 1, 2)}$$

最後に、冒頭で定義した関数Lを\(w_{1 2}\)で偏微分する式に計算結果を当てはめていきます.(以下に再掲します)
$$\displaystyle\frac{\partial L}{\partial w_{12}} = \displaystyle\frac{\partial L}{\partial u_{1}}\cdot \displaystyle\frac{\partial u_{1}}{\partial w_{12}}$$

誤差ベクトルydを定義します.
$$yd= {yp_{1}}-yt_{1}$$

式に代入します.
$$\displaystyle\frac{\partial L}{\partial w_{12}} = x_{2}\cdot yd_{1}$$

更に添え字などを戻して式を一般化します.
$$\displaystyle\frac{\partial L}{\partial w_{ij}} = \displaystyle\frac{1}{M}\sum\limits_{m=0}^{M-1} x_{j}^{(m)}\cdot yd_{i}^{(m)} $$

以上が多値分類における損失関数の偏微分結果(勾配関数)となります.

勾配降下法の適用

$$w_{ij}^{(k+1)} = w_{ij}^{(k)}- \displaystyle\frac{1}{M}\sum\limits_{m=0}^{M-1} x_{j}^{(m)}\cdot yd_{i}^{(m)} \displaystyle_{(i,j = 0, 1, 2)}$$

終わりに

　今回は多値分類についてまとめました.
考え方としては２値分類のベクトル→行列に拡張しただけではあるものの、iやjなどの添え字も増えそれ以上に複雑に感じるかもしれません.
しかし、勾配降下法をベースに２値分類、多値分類、ディープラーニング(画像認識)..と応用が利いているので、最初の壁を乗り越えればあとは知見の拡張がメインになっていきます. ベースがぶれないように意識して取り組んでいきましょう.
　前回もですが、実際にプログラムとして組み込んだ例題があるとより理解が深まると思うので、サンプルでよく使われる「iris data set」などを用いた実装方法を次回にでもまとめていけたらと思います.(順当に行けば次はディープラーニングなんですが「LaTex」で数式を打ち込んでいくのが割と苦痛なので箸休めの意味も込めて…)