[Raspberry pi]Pythonで機械学習備忘録(3)〜実装
- 2020.10.02
- IoT
![[Raspberry pi]Pythonで機械学習備忘録(3)〜実装](https://kocoffy.com/programmer_cat/wp-content/uploads/2020/09/機械学習.jpg)
前回の続きです.
今回でいよいよラスト(の予定)となります.
(当初の計画通りラズパイ上に表示させます.)
環境
・OS:
Raspbian(Raspberry pi4 4GB)
・言語:
Python 3.7
・使用ライブラリ:
matplotlib
numpy
pandas
sklearn
・使用するデータセット:
Boston house-prices (ボストン市の住宅価格)
ボストン郊外地域の不動産物件に関する統計データが入っています.
scikit-learnから呼び出せます.
以下にその他呼び出せるデータセットがまとめられていました.
scikit-learn に付属しているデータセット
実装(計算)
前回導出した式を参考に計算部分をまとめたクラスを作成しました.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 |
from matplotlib import pyplot as plt import numpy as np import pandas as pd from sklearn.linear_model import LinearRegression from sklearn.datasets import load_boston # サンプルを利用 def boston(): bsdata = load_boston() df = pd.DataFrame(bsdata.data, columns=bsdata.feature_names) df['Price'] = bsdata.target # Price列を取得 # x_data = pd.DataFrame(df['Price']) # RM列を取得 # y_data = pd.DataFrame(df['RM']) return df #CSV読込(データフレーム) def csvToDf(csv): df = pd.read_csv(csv) return df # sklearnで単回帰 def regression(x_data, y_data): model_lr = LinearRegression() model_lr.fit(x_data, y_data) print('モデル関数の回帰変数 w1:,', model_lr.coef_) print('モデル関数の切片 w2:', model_lr.intercept_) print('y= %.3fx + %.3f' % (model_lr.coef_ , model_lr.intercept_)) print('決定係数 R^2: ', model_lr.score(x_data, y_data)) plt.figure("sklearn") plt.grid() # グリッド(目盛り線)を表示 plt.plot(x_data, y_data, 'o') plt.plot(x_data, model_lr.predict(x_data), linestyle="solid") plt.show() # 回帰モデル def reg(w0, w1, x, e=0): y = w0 + w1 * x + e print('y= %.3fx + %.3f' % (w1, w0)) return y # dataframeをnumpyに変換 def dfToNp(df): df_np = df.values df_np = df_np.T[0] print('dfをnpに変換:', df_np) return df_np # xの分散、yの分散、xyの共分散を導出 def distributed(x_np, y_np): xy_np = np.stack([x_np, y_np]) xx_s = np.var(x_np) yy_s = np.var(y_np) xy_s = np.cov(xy_np, rowvar=1, bias=1) s = [xx_s, yy_s, xy_s] print('xの分散を作成:', s[0]) print('yの分散を作成:', s[1]) print('x,yの共分散を作成') print(s[2]) return s # 回帰係数を導出 def coefficientReg(x_np, y_np, xx_s, xy_s): w_1 = xy_s[0][1] / xx_s print('回帰係数(w1) :', w_1) w_0 = np.mean(y_np) - w_1 * np.mean(x_np) print('w0 :', w_0) return [w_0, w_1] # # model_lr.predict(self.x_data) = (self.w_0 + (self.w_1 * self.x_np)) # plt.grid() # グリッド(目盛り線)を表示 # # グラフ表示 # plt.plot(self.x_data, self.y_data, 'o') # # 単回帰直線表示 # plt.plot(self.x_data, self.reg(self.w_0, self.w_1, self.x_np), linestyle="solid") # plt.show() # 全変動 def SST(y_np): # y - y_ sst = ((y_np - np.mean(y_np)) ** 2).sum() return sst # 回帰変動 def SSR(w_0, w_1, x_np, y_np): # y^ = w0 + w1*x^ # y^ - y_ ssr = (((w_0 + (w_1 * x_np)) - np.mean(y_np)) ** 2).sum() return ssr # 残差変動 def SSE(w_0, w_1, x_np, y_np): # y - y^ sse = ((y_np - (w_0 + (w_1 * x_np))) ** 2).sum() return sse # 決定係数 def decision(sst, ssr, sse, xx_s, yy_s, xy_s): print('SST:', sst) print('SSR:', ssr) print('SSE:', sse) print('SST = SSR + SSEである事を確認:%.3f + %.3f = %.3f' % (ssr, sse, ssr + sse)) # 決定係数(R^2) R2 = ssr / sst print("決定係数(R^2) = ", R2) # 相関係数 r = (xy_s[0][1] / (xx_s * yy_s) ** 0.5) ** 2 print("相関係数(r^2) = ", r) return R2 |
また、確認用にscikit-learnライブラリを使って分析する関数も組み込んでいます.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# sklearnで単回帰 def regression(x_data, y_data): model_lr = LinearRegression() model_lr.fit(x_data, y_data) print('モデル関数の回帰変数 w1:,', model_lr.coef_) print('モデル関数の切片 w2:', model_lr.intercept_) print('y= %.3fx + %.3f' % (model_lr.coef_ , model_lr.intercept_)) print('決定係数 R^2: ', model_lr.score(x_data, y_data)) plt.figure("sklearn") plt.grid() # グリッド(目盛り線)を表示 plt.plot(x_data, y_data, 'o') plt.plot(x_data, model_lr.predict(x_data), linestyle="solid") plt.show() |
呼び出しクラス(main.py)
上記ソースを呼び出すmainコードです.
使えるだけ全部呼び出してます.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
from matplotlib import pyplot as plt import regression as reg import pandas as pd #回帰モデル汎用ライブラリ使用 class Application(): def __init__(self, master=None): # ボストンデータセットからデータフレームとして取得 df = reg.boston() x_data = pd.DataFrame(df['Price']) y_data = pd.DataFrame(df['RM']) # reg.regression(x_data, y_data) #numpyに変換 x_np = reg.dfToNp(x_data) y_np = reg.dfToNp(y_data) # x,yの分散、xyの共分散を取得 S = reg.distributed(x_np, y_np) # w_0,w_1を取得 W = reg.coefficientReg(x_np, y_np, S[0], S[2]) # グラフ表示 plt.figure("numpy") plt.grid() # グリッド(目盛り線)を表示 plt.plot(x_data, y_data, 'o') # 単回帰直線表示 plt.plot(x_data, reg.reg(W[0], W[1], x_np), linestyle="solid") plt.show() SST = reg.SST(y_np) SSR = reg.SSR(W[0], W[1], x_np, y_np) SSE = reg.SSE(W[0], W[1], x_np, y_np) R2 = reg.decision(SST, SSR, SSE, S[0], S[1], S[2]) if __name__ == '__main__': Application() |
動作画面
実行してみます.
|
1 |
$ python 3.7 main.py |
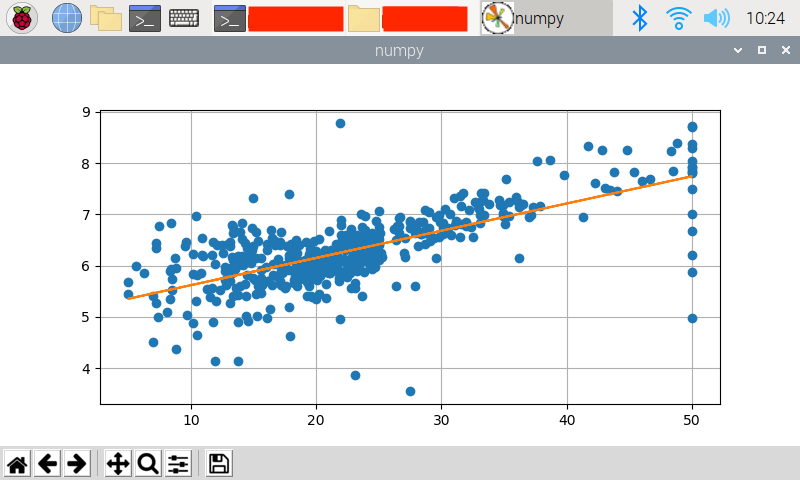
以下はログです.
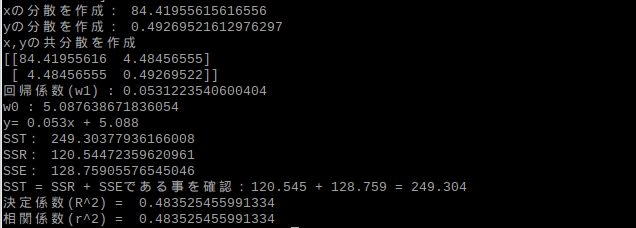
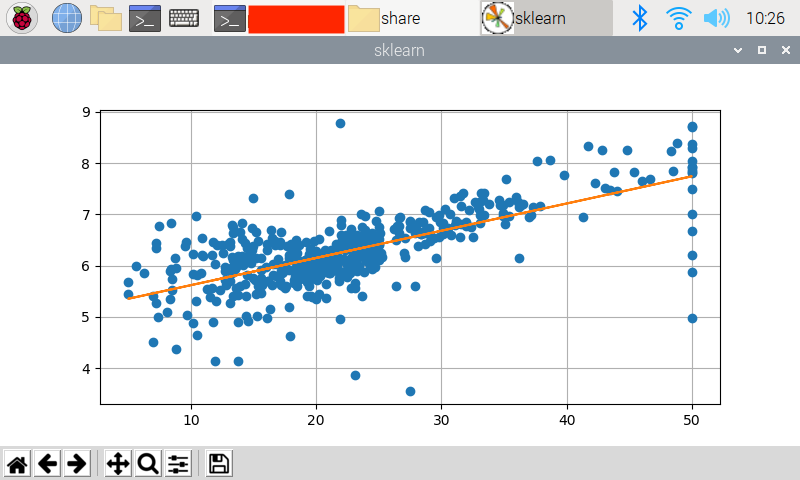
また、確認用に実装していたscikit-learnを使った分析結果も載せておきます.
ログです.
回帰係数と直線の式、決定係数がnumpyで導出した場合とほぼ同じになっていますね.

終わりに
今回、一から機械学習について勉強を行ったわけですが、理解に時間をかけたその分scikit-learnライブラリで2〜3行で単回帰分析ができることの驚きが大きく感じてしまいました..
コーディングの際も参考にさせて頂いた方々はもちろんいらっしゃいますが、pandasによる配列操作(データセット)やnumpyによる計算方法もシンプルに実現できたため、改めてPythonの凄み実感しています.
数学における途中計算部分を大幅にカットできるのは勉強する上で非常に心強かったです.
逆に、中身を理解する前にものが完成してしまうスピード感はしっかり意識した上で勉強に役立てていきたいとも思います.(達成感でやる気が落ちちゃうので…)
と、前回までで機械学習に関して思うところは吐き出し尽くしていることもありまして、本実装は意外とあっさりしていたため最後もこんな感じの感想しかありません.
基礎的なモデルに四苦八苦していたわけですが、せっかくなら重回帰からのロジスティック回帰…と理解を深めていきたいとも考えているので、次は勾配降下法についてこれから少しずつ勉強していこうかと思います.
ここまで読んで頂きありがとうございます.
-
前の記事
![[Raspberry pi]Pythonで機械学習備忘録(2)〜単回帰,最小二乗法](https://kocoffy.com/programmer_cat/wp-content/uploads/2020/09/機械学習-150x150.jpg)
[Raspberry pi]Pythonで機械学習備忘録(2)〜単回帰,最小二乗法 2020.09.29
-
次の記事

JuliusForAndroidを動かしてみる 2020.10.05