[Raspberry pi]Pythonで機械学習備忘録(2)〜単回帰,最小二乗法
- 2020.09.29
- IoT
![[Raspberry pi]Pythonで機械学習備忘録(2)〜単回帰,最小二乗法](https://kocoffy.com/programmer_cat/wp-content/uploads/2020/09/機械学習.jpg)
前回に引き続き、今回は実際に回帰モデルの計算方法をまとめていきます.
計算方法がわかれば、いよいよプログラムとしてラズパイ に組み込めます.
また、僕自身も約高校ぶりに真面目に計算をしているた途中式なども少し詳細に書いています.
ちなみにこちらの書籍で機械学習に必要な数学を学んでいます.
単回帰
1つの入力に対して1つの出力を予測するモデルです.
機械学習における初期中の初期ということからまずはここから調べていきます.
単回帰モデルの予測式は以下のような一次関数になります.
予測式:\(y_p = w_0 + w_1 * x \)\(\\\) \(y_p\):予測値\(\\\) \(w_0\):定数項\(\\\) \(w_1\):係数パラメータ\(\\\) \(x\):説明変数ただし、分散している値が1本の直線で結び付くわけがないため、これに誤差を追加することで正解の式とする.
\(y_t = w_0 + w_1 * x + ε\)\(\\\) \(y_t:\)正解値\(\\\) \(ε\)(エプシロン):残差ここで定義した式と変数をベースにして直線を推定していきます.
最小二乗法
まず初めに最小二乗和(残差平方和)を説明します.
最初に公式を載せます.
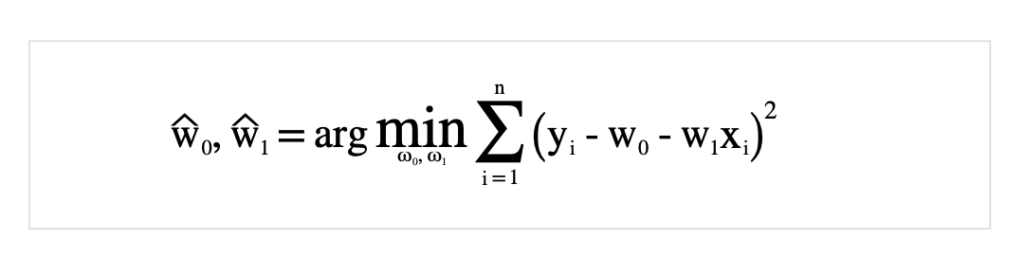
正解値と予測値の差を誤差とした場合、どちらかが負の値だと正確な誤差が出せません.
そういった問題を解消するために、各座標ごとに「正解値と予測値の差の二乗」をとります.
ではどのようにして最小値を求めて行くのかを以下の「最小二乗推定量」の項より説明していきます.
補足
ちなみに\(w_0、w_1\)の頭についている記号はハットと言います. 予測値を表す記号です.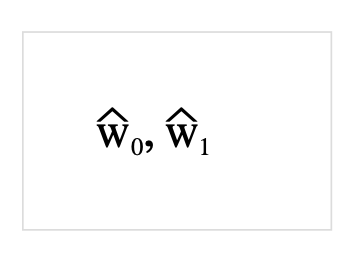
単回帰の項目で載せた式をハットを用いて表現すると以下のようになります.

最小二乗推定量
\(w_0,w_1\)の最小値はそれぞれ(\(w_0,w_1\))の偏微分が0になる時の値です. 実際に最小二乗法の式を展開しつつ、整理していきます. 最小二乗和を以下のようにおきます.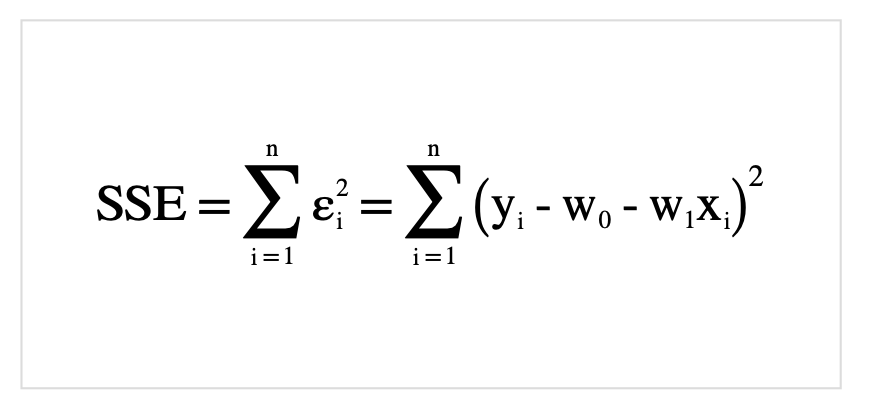
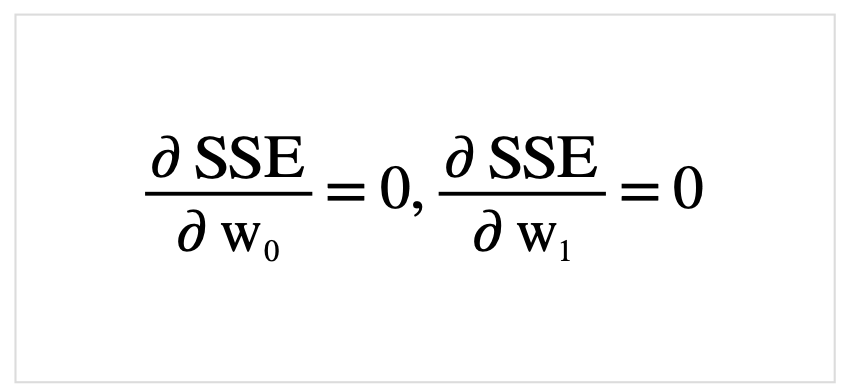
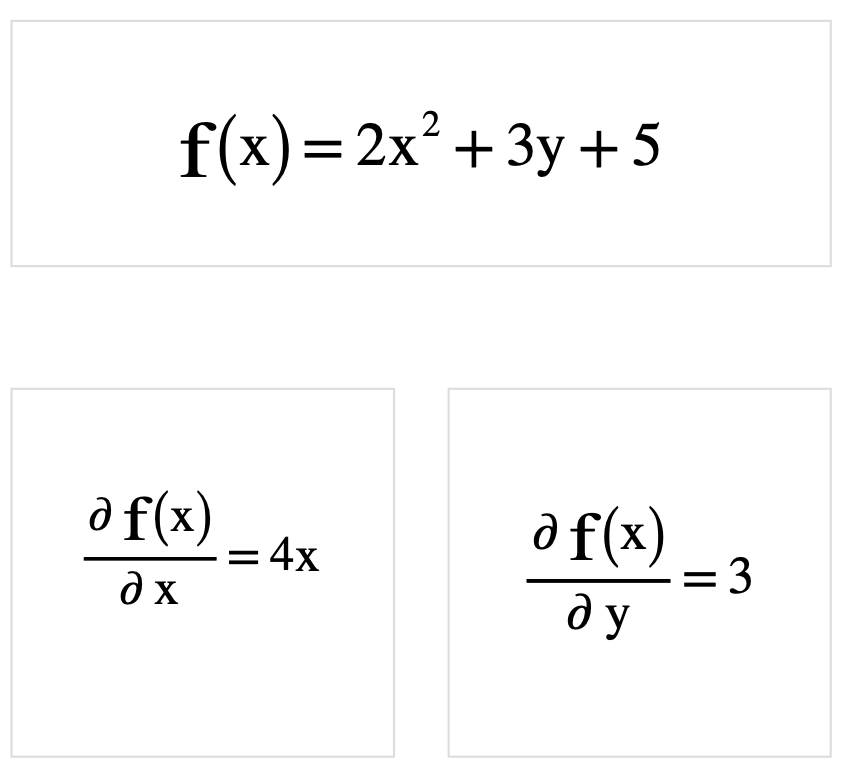
それでは先ほど定義した式SSEを展開していきましょう.



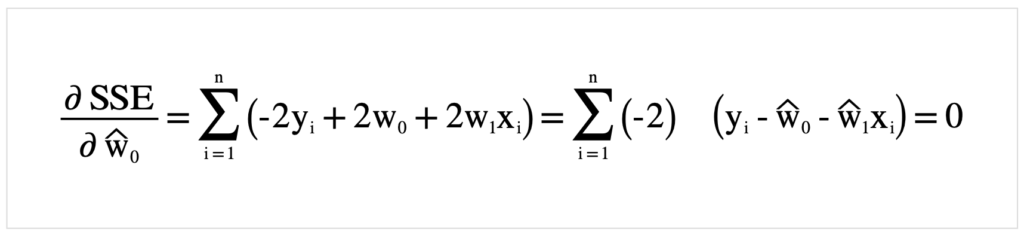
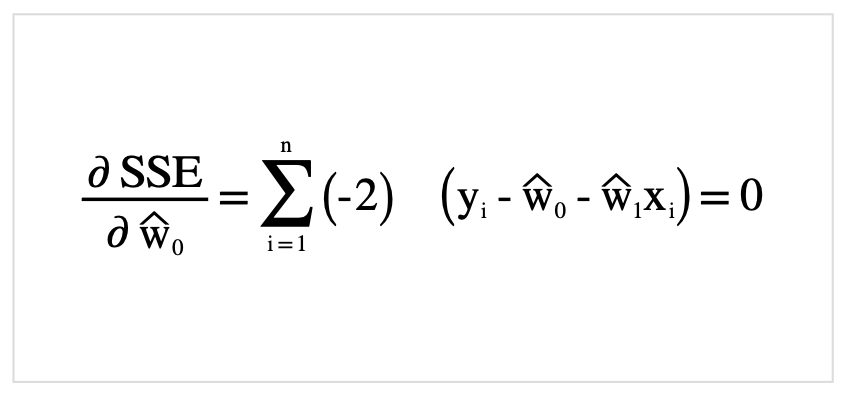
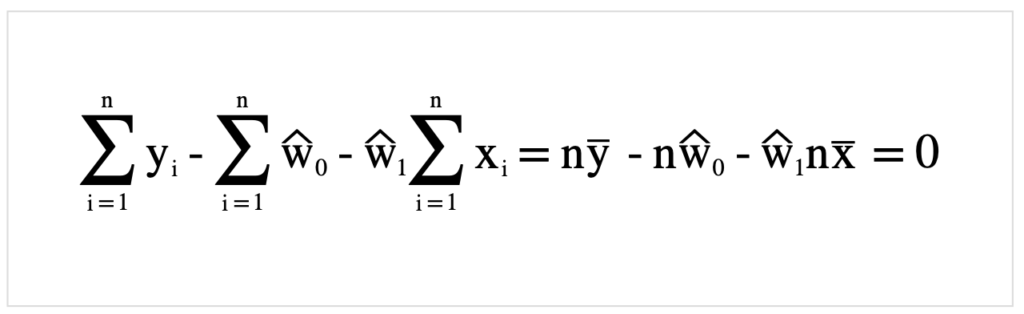
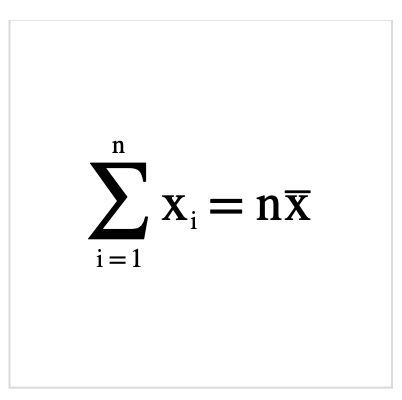
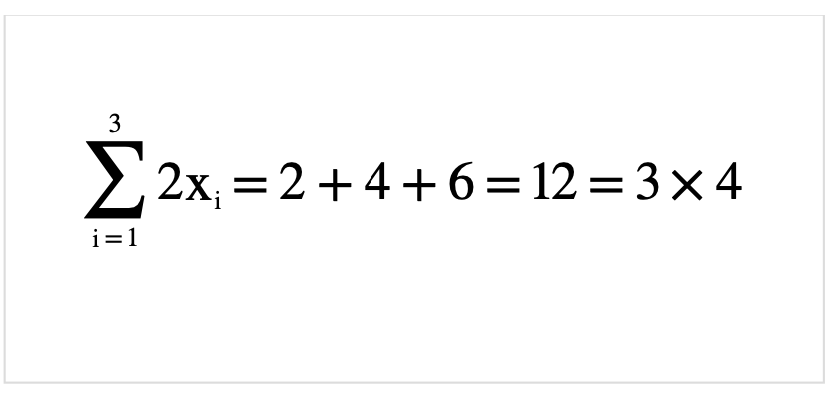
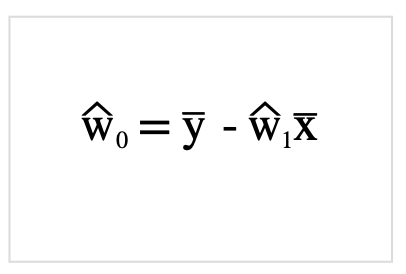
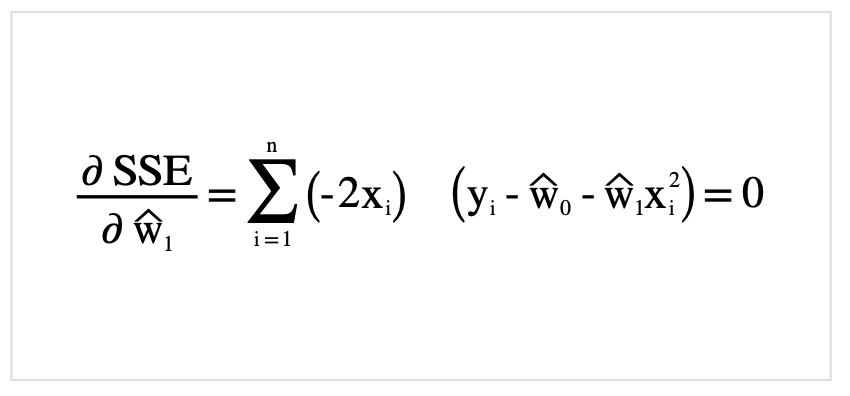

さらに整理.
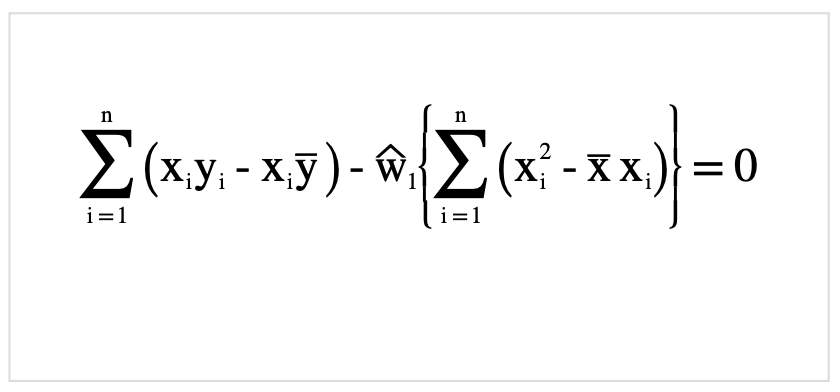
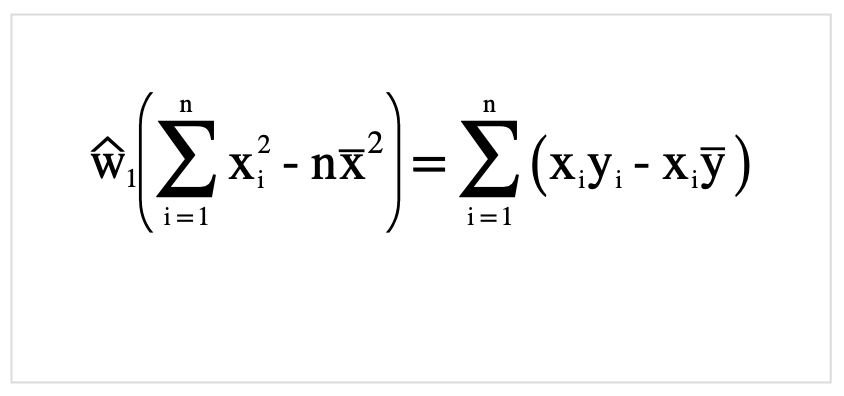
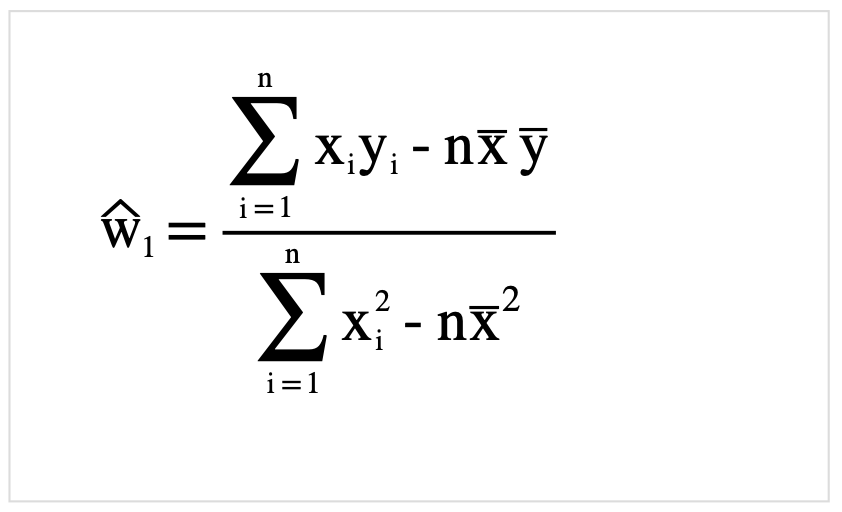
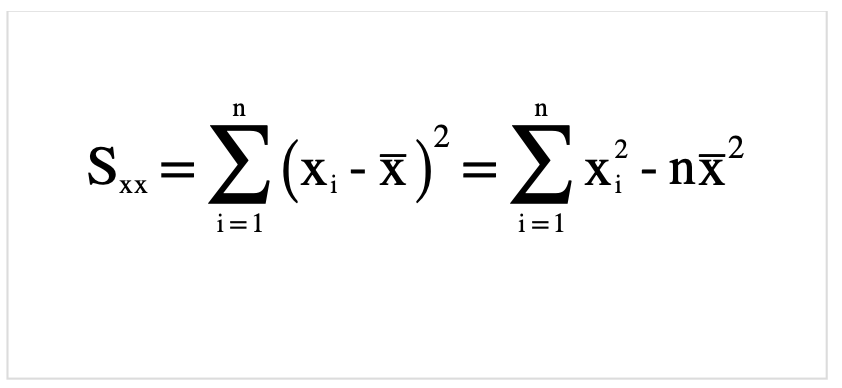
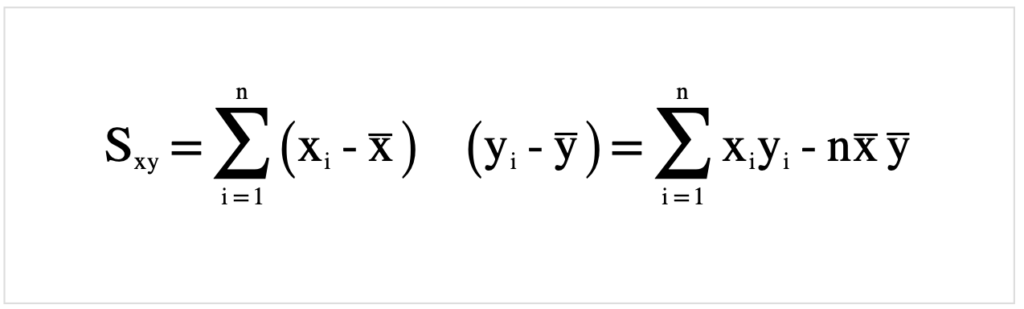
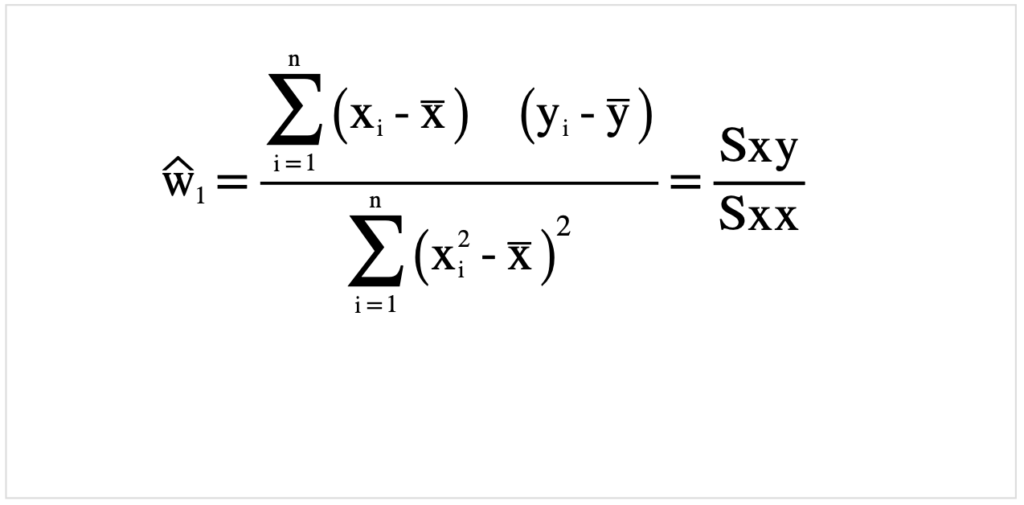
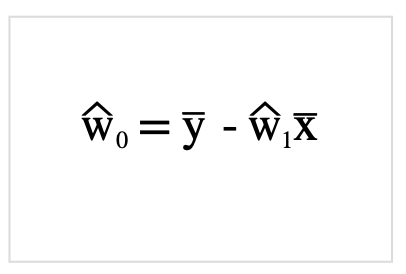
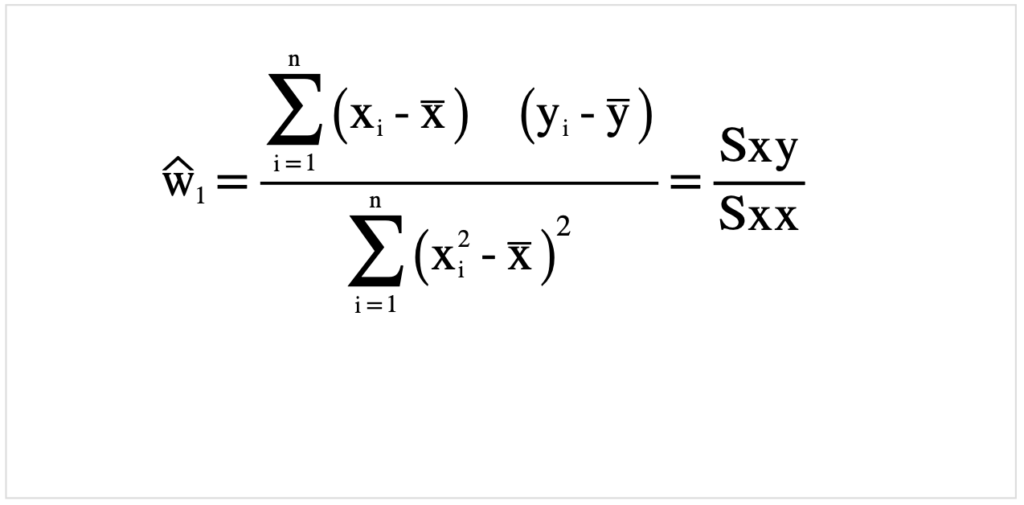
決定係数
予測式が理想の式とどのくらい一致しているのか知っておく必要があります.
そのための指標として、「決定係数」(R)があります.
「決定係数」値の範囲は0〜1となっており、1に近いほど理想に近いと判断できます.
また、相関係数(r)とはイコール(厳密には相関係数を2乗する)の関係にあります.
回帰変動が全変動に対してどれくらいの影響を与えているかの係数でもあり、その全変動(SST)は回帰変動(SSR)と残差変動(SSE)の合計になります.
以上の点を踏まえ計算式を以下に載せます.
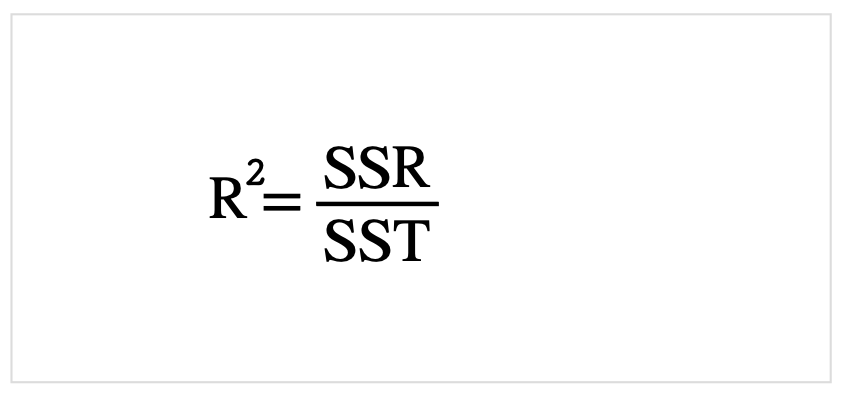
決定係数と相関係数との関係式は以下です.
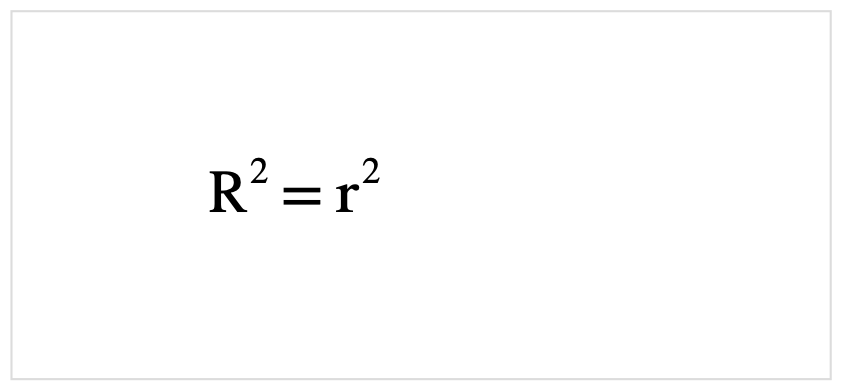
また、ついでに相関係数の公式も載せておきます.
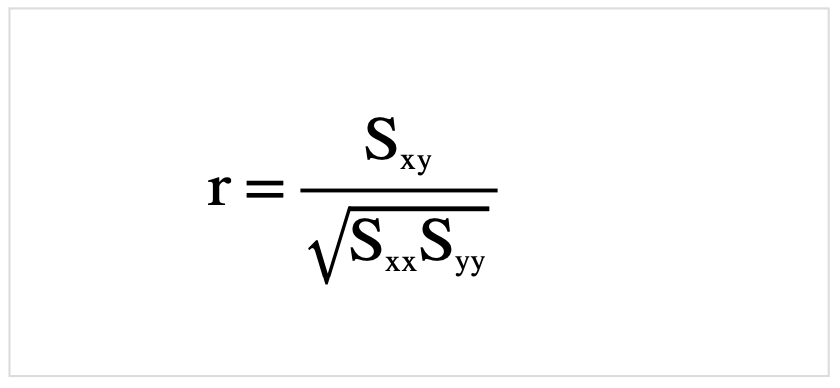
決定係数、相関係数に関しては以下のサイトが分かりやすかったです.
相関係数Rと決定係数R2
分散分析
最後です.分散分析に関しては決定係数の項で登場しています.
ここでは式のみ紹介します.
全変動(SST)

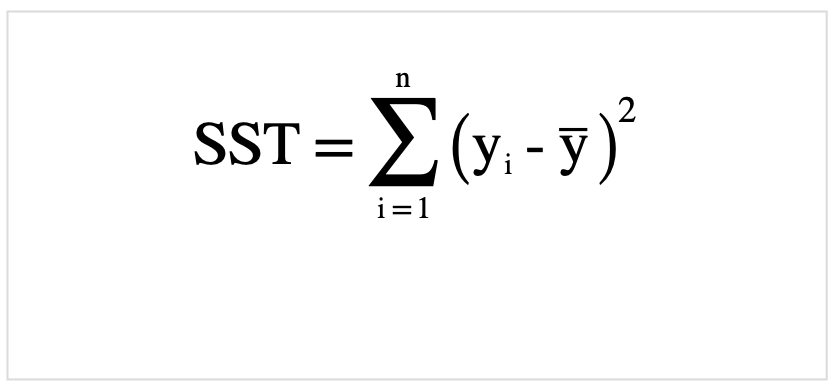
回帰変動(SSR)
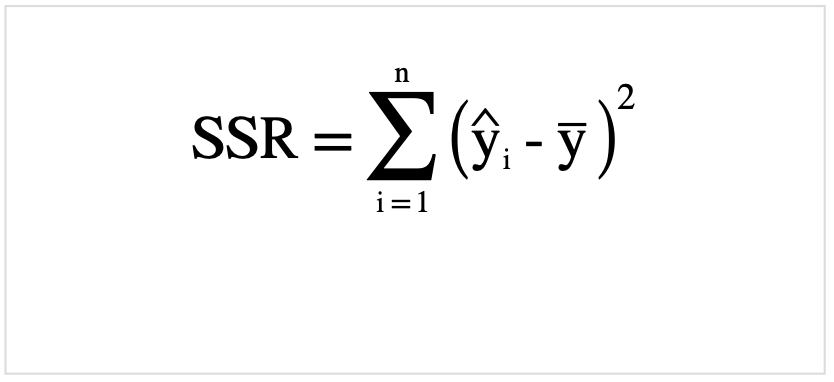
残差変動(SSE)
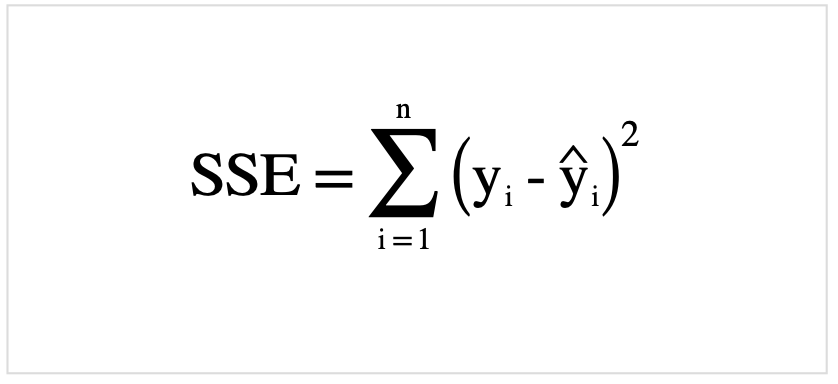
詳しくは以下を参考にしてください.
全変動,回帰変動,残差変動の意味と関係
終わりに
今回は主に数学的な部分をまとめてきました.
ここら辺に関しては読んで理解するというよりは実際に紙とペンで計算して理解していきました.
久々だったのもあってだいぶ苦戦しましたが、後はここで導出した式をコードに書き起こしていくだけです.
ここまで見ていただきありがとうございます.
-
前の記事
![[Raspberry pi]4インチLCDタッチモニター](https://kocoffy.com/programmer_cat/wp-content/uploads/2020/09/組み立てた-150x150.jpeg)
[Raspberry pi]4インチLCDタッチモニター 2020.09.28
-
次の記事
![[Raspberry pi]Pythonで機械学習備忘録(3)〜実装](https://kocoffy.com/programmer_cat/wp-content/uploads/2020/09/機械学習-150x150.jpg)
[Raspberry pi]Pythonで機械学習備忘録(3)〜実装 2020.10.02